Question

Two cards are selected from a standard deck of 52 playing cards. The first card is not replaced before the second card is selected. Find the probability of selecting a four and then selecting a king.

Answer 1

0.006%.

Explanation:

In a standard deck of cards, there should be four 4 cards and four king cards. We first want the probability of selecting a 4 card, which is just

`$(4)/(52).$`

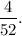
Then we want it for the king card, but since we didn't replace the first card, we only have 51 cards left. This implies our probability is

`$(4)/(51).$`

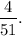
Now, all we have left is to multiply the two fractions and divide by the denominator:

`$(4)/(52) \cdot (4)/(51) = (16)/(2652) = (4)/(663) = 0.006.$`