Question

For the equation y=2x2-16x+30 Identify the vertex and convert into vertex form. Create an inverse function.

Answer 1

Vertex: (4, -2)

Vertex form:
`y = 2(x-4)^2 - 2`

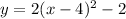
Inverse function:
`y = (16 \pm√(16+8x))/4`

Explanation:

The x-coordinate of the vertex can be calculated using the formula:

`x_(vertex) = -b/2a`

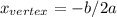
Where a and b are coefficients of the quadratic equation in the form:

`y = ax^2 + bx + c`

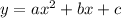
So, using a = 2 and b = -16, we have:

`x_(vertex) = 16/4 = 4`

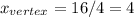
To find the y-coordinate of the vertex, we calculate y using the x-coordinate of the vertex:

`y=2*4^2-16*4+30`

`y = -2`

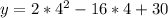
So the vertex is (4, -2)

The vertex form is given by:

`y = a(x-h)^2 + k`

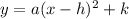
Where h is the x-coordinate of the vertex and k is the y-coordinate of the vertex. Therefore, we have that:

`y = 2(x-4)^2 - 2`

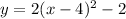
To create an inverse function, we switch x by y and vice-versa:

`x=2y^2-16y+30`

`2y^2-16y+30 - x = 0`

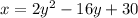
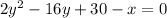
Then, using Bhaskara's formula, we have:

`\Delta = b^2 -4ac = (-16)^2 - 4*2*(30-x) = 16 + 8x`

`y = (-b \pm√(\Delta))/2a`

`y = (16 \pm√(16+8x))/4`

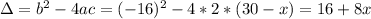
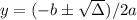
It's important to say that this inverse function is not really a function, because one value of x gives two values of y.