Answer:
a) Flow rate if the pipe is horizontal, Q = 4.69 * 10⁻³ ft³/s
b) Flow rate if the pipe is vertical, Q = 3.30 * 10⁻³ ft³/s
Step-by-step explanation:
From the BI table, dynamic viscosity of water at 120°F is:

Pressure gradient,
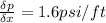
Pipe Diameter, D = 2 in = 2/12 ft = 0.167 ft
Dynamic viscosity of asphalt at 120°F:
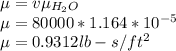
Specific weight of asphalt:
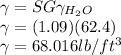
Flow rate, Q, of the asphalt when the pipe is in horizontal position assuming that the flow is laminar:
Note that if the pipe is horizontal, θ = 0°
![Q = (\pi D^4)/(128 \mu) [((\delta p )/(\delta x)) - \gamma sin \theta]\\\\Q = (\pi 0.167^4)/(128 * 0.9312) [(1.6*144) - 68.016 sin (0)]\\\\Q = 4.69 * 10^(-3) ft^3 / s](https://img.qammunity.org/2021/formulas/engineering/college/1tg9stdpzgoffl43icp9kyer9gw96iha35.png)
b) Flow rate assuming the pipe is vertical:
At vertical pipe position, θ = 90°
![Q = (\pi D^4)/(128 \mu) [((\delta p )/(\delta x)) - \gamma sin \theta]\\\\Q = (\pi 0.167^4)/(128 * 0.9312) [(1.6*144) - 68.016 sin (90)]\\\\Q = 3.30 * 10^(-3) ft^3 / s](https://img.qammunity.org/2021/formulas/engineering/college/ykrvaimequyxysx1xk31m6p18ukszwhi5a.png)