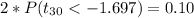Answer:
a) The degrees of freedom are given by:
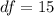
And the rejection region is
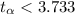
And the significance level would be:

b) The degrees of freedom are given by:

And the rejection region is
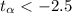
And the significance level would be:

c) The degrees of freedom are given by:
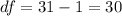
And the rejection region is
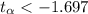 or
or
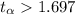
And the significance level would be:
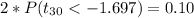
Explanation:
Part a
We have the following system of hypothesis:
Null hypothesis:
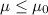
Alternative hypothesis:
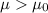
The degrees of freedom are given by:
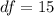
And the rejection region is
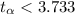
And the significance level would be:

Part b
We have the following system of hypothesis:
Null hypothesis:
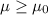
Alternative hypothesis:
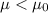
The degrees of freedom are given by:

And the rejection region is
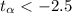
And the significance level would be:

Part c
We have the following system of hypothesis:
Null hypothesis:
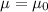
Alternative hypothesis:
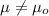
The degrees of freedom are given by:
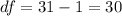
And the rejection region is
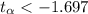 or
or
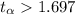
And the significance level would be: