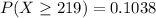Answer:
4
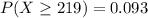
5
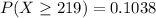
Explanation:
From the question we are told that
The percentage of hair dryers that are defective is p=2%
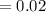
The sample size is
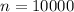
The random number is x = 219
The mean of this data set is evaluated as
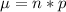
substituting values
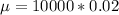
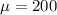
The standard deviation is evaluated as
![\sigma = √([\mu (1 -p)])](https://img.qammunity.org/2021/formulas/mathematics/college/6n2sr4tgckv9qg9mq6pbregm541zct1oz8.png)
substituting values
![\sigma = √([200 (1 -0.02)])](https://img.qammunity.org/2021/formulas/mathematics/college/j6okxftrzlfwmjtipxndumn11q3e31ntil.png)
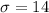
Since it is a one tail test the degree of freedom is
df = 0.5
So
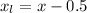

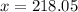
Now applying normal approximation
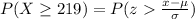
substituting values
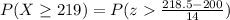
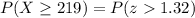
From the z-table
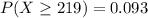
Considering Question 5
The random number is x = 90
The mean is

Where n = 100
and p = 0.85
So
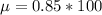
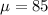
The standard deviation is evaluated as
![\sigma = √([\mu (1 -p)])](https://img.qammunity.org/2021/formulas/mathematics/college/6n2sr4tgckv9qg9mq6pbregm541zct1oz8.png)
substituting values
![\sigma = √([85 (1 -0.85)])](https://img.qammunity.org/2021/formulas/mathematics/college/4fhgzzgbsc1udc4ogb739xd8myjwep7maa.png)
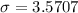
Since it is a one tail test the degree of freedom is
df = 0.5
Now applying normal approximation
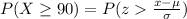
substituting values
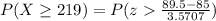

From the z-table