Question

Air enters the compressor of a cold air-standard Brayton cycle with regeneration and reheat at 100 kPa, 300 K, with a mass flow rate of 6 kg/s. The compressor pressure ratio is 10, and the inlet temperature for each turbine stage is 1400 K. The pressure ratios across each turbine stage are equal. The turbine stages and compressor each have isentropic efficiencies of 80% and the regenerator effectiveness is 80%. For k= 1.4.

Calculate:
a. the thermal efficiency of the cycle.
b. the back work ratio.
c. the net power developed, in kW.

Answer 1

a. 47.48%

b. 35.58%

c. 2957.715 KW

Step-by-step explanation:

`T_2 =T_1 + (T_(2s) - T_1)/(\eta _c)`

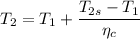
T₁ = 300 K

`(T_(2s))/(T_1) = \left( (P_(2))/(P_1) \right)^{(k-1)/(k) }`

`T_(2s) = 300 * (10) ^{(0.4)/(1.4) }`

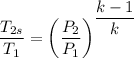
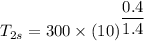
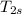`T_(2s)` = 579.21 K

T₂ = 300+ (579.21 - 300)/0.8 = 649.01 K

T₃ = T₂ +
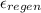`\epsilon _(regen)`(T₅ - T₂)

T₄ = 1400 K

Given that the pressure ratios across each turbine stage are equal, we have;

`(T_(5s))/(T_4) = \left( (P_(5))/(P_4) \right)^{(k-1)/(k) }`

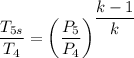
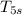`T_(5s)` = 1400×
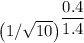`\left( 1/√(10) \right)^{(0.4)/(1.4) }` = 1007.6 K

T₅ = T₄ + (
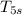`T_(5s)` - T₄)/
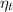`\eta _t` = 1400 + (1007.6- 1400)/0.8 = 909.5 K

T₃ = T₂ +
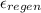`\epsilon _(regen)`(T₅ - T₂)

T₃ = 649.01 + 0.8*(909.5 - 649.01 ) = 857.402 K

T₆ = 1400 K

`(T_(7s))/(T_6) = \left( (P_(7))/(P_6) \right)^{(k-1)/(k) }`

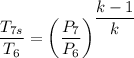
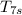`T_(7s)` = 1400×
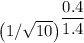`\left( 1/√(10) \right)^{(0.4)/(1.4) }` = 1007.6 K

T₇ = T₆ + (
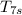`T_(7s)` - T₆)/
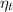`\eta _t` = 1400 + (1007.6 - 1400)/0.8 = 909.5 K

a.
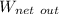`W_(net \ out)` = cp(T₆ -T₇) = 1.005 * (1400 - 909.5) = 492.9525 KJ/kg

Heat supplied is given by the relation

cp(T₄ - T₃) + cp(T₆ - T₅) = 1.005*((1400 - 857.402) + (1400 - 909.5)) = 1038.26349 kJ/kg

Thermal efficiency of the cycle = (Net work output)/(Heat supplied)

Thermal efficiency of the cycle = (492.9525 )/(1038.26349 ) =0.4748 = 47.48%

b.
`bwr = (W_(c,in))/(W_(t,out))`

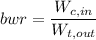
bwr = (T₂ -T₁)/[(T₄ - T₅) +(T₆ -T₇)] = (649.01 - 300)/((1400 - 909.5) + (1400 - 909.5)) = 35.58%

c. Power = 6 kg *492.9525 KJ/kg = 2957.715 KW