Question

A statistics pratitioner took a random sample of 30 observations from a population whose standard deviation is 15 and computed the sample mean to be 50. The 90% confidence inverval for the mean will be ____________ and ______________.

Answer 1

`50-1.64(15)/(√(30))=45.509`

`50+1.64(15)/(√(30))=54.491`

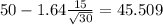
The 90% confidence inverval for the mean will be 45.509 and 54.491

Explanation:

Information given

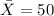`\bar X= 50` represent the sample mean

`\mu` population mean (variable of interest)

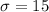`\sigma= 15` represent the sample standard deviation

n= 30 represent the sample size

Confidence interval

The confidence interval for the mean is given by the following formula:

`\bar X \pm z_(\alpha/2)(\sigma)/(√(n))` (1)

Since the Confidence is 0.90 or 90%, the value of
`\alpha=0.1` and
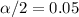`\alpha/2 =0.05`, the critical value would be
`z_(\alpha/2)=1.64`

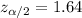
Now we have everything in order to replace into formula (1):

`50-1.64(15)/(√(30))=45.509`

`50+1.64(15)/(√(30))=54.491`

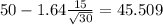
The 90% confidence inverval for the mean will be 45.509 and 54.491