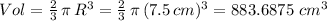Answer:
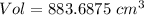
Explanation:
Recall that the volume of a whole sphere is given by the formula:
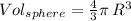
then, the volume of a semi-sphere would be half of the formula above:
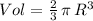
Now, the radius R is given by half of the semi-sphere diameter: 15/2 = 7.5 cm.
which makes our calculation: