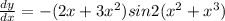Answer:
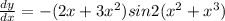
Explanation:
Step(i):-
Given y = cos² (x² + x³) ....(i)
By using differentiation formulas
a)
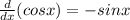
b)
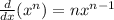
Step(ii):-
Differentiating equation (i) with respective to 'x'
First apply formula
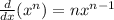
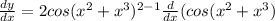
Now we will apply formula
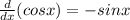
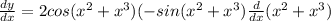
Again apply formula
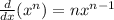
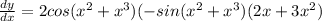
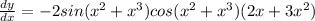
we know that trigonometric formulas
Sin 2θ = 2 sinθ cosθ
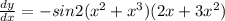
Final answer:-