Question

Given: circle C is constructed so that CD = DE = AD;—

CA is the radius of circle C

Prove: AE is tangent to c

Answer 1

Explanation:

16. m<CAD + m<DAE =
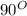`90^(O)` - Definition of complementary angles

18. m<CAD + m<DAE = m<CAE =
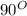`90^(O)` - Substitution property

20. m<CAE =
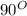`90^(O)` - Definition of perpendicular

21. AE ⊥ AC - AE is tangent to circle C

To prove that AE is tangent to C. Given that CA is the radius of circle C,

Then,

m<CAD + m<DAE =
`90^(O)`

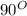
So that,

AE ⊥ AC

Thus, AE is tangent to C.