Answer:
h = 0.047 m
Step-by-step explanation:
It is given that,
Radius of an air bubble is 0.0003 m
The surface tension of water is

We need to find the depth at which an air bubble of radius 0.0003 m will remain in equilibrium in water. Let it is given by h.
Pressure due to surface tension is given by :
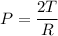 .....(1)
.....(1)
T is surface tension
Also, pressure due to a height is given by :
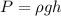
So, equation (1) becomes :

So,
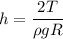
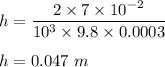
So, the depth is 0.047 m.