Question

A spherical raindrop evaporates at a rate proportional to its surface area. Write down a differ- ential equation for its volume as a function as a function of time. Solve this equation, and find the constant of proportionality if a 1cm3 raindrop takes 10 seconds to evaporate.

Answer 1

`(dV)/(dt) =-4 \pi k ((3)/(4 \pi))^(2)/(3) }}V^{(2)/(3)}`

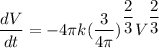
k = 3.022

Explanation:

Given that:

A spherical raindrop evaporates at a rate proportional to its surface area.

The surface area SA of a spherical object is given by the relation:

SA = 4πr²

Write down a differ- ential equation for its volume as a function as a function of time.

So; to differentiate Volume (V) in respect to time (t) ;then:

`(dV)/(dt) =-k( 4 \pi r^2)`

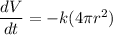
Likewise; we know known that the volume of a sphere V =
`(4)/(3) \pi r^3`

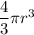
Thus, from above;

`3V = 4 \pi r^3`

`(3V)/(4 \pi) = r^3`

`r^3 = ((3)/(4 \pi ))^{(2)/(3)}V^{(2)/(3)}`

`r^2 = 4 \pi( (3)/(4 \pi))(2)/(3)V(2)/(3)`

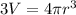
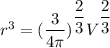
Thus; solving the differential:

`(dV)/(dt) =-k( 4 \pi * 4 \pi( (3)/(4 \pi))(2)/(3)V(2)/(3))`

`(dV)/(dt) =-4 \pi k ((3)/(4 \pi))^(2)/(3) }}V^{(2)/(3)}`

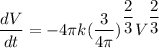
So;

we are to find the constant proportionality K

If Volume V = 1 cm³ and the time = 10 sec

`(1)/(10) =-4 \pi k ((3)/(4 \pi))^(2)/(3) }}(1)^{(2)/(3)}`

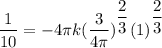
0.1 = - 4π k (0.3848 × 1)

0.1 = - 4π k × 0.3848

4π k = 0.3848/0.1

4π k = 3.848

k = 3.848/4π

k = 3.022