Question

A farmer with 600 ft of available fencing wants to enclose a rectangular are located adjacent to a farmhouse (with no fencing required along the farmhouse) and then divide it into four sections with fencing perpendicular to the side of the farmhouse. Show that the largest possible area of the four sections will be 18,000 square feet, and state the corresponding dimensions of the rectangular area.

Answer 1

The corresponding dimensions will be "x = 300 & y = 60".

Step-by-step explanation:

Available fencing = 600 ft

Fencing,

⇒
`5y+x=600`

⇒
`x=600-5y`

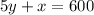
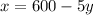
As we know,

⇒
`Area =xy`

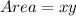
On substituting the given values, we get

`=(600-5y)y`

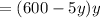
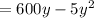`=600y-5y^2` ...(equation 1)

On differentiating with respect to y, we get

⇒
`(dA)/(dy) =600-10y`

`0 = 600-10y`

`600=10y`

`y=(600)/(10)`

`y=60`

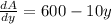
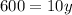
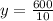
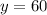
On putting the values of y in equation 1, we get

⇒
`600(60)-5(60)^2`

⇒
`600(60)-5(3600)`

⇒
`36000 - 18000`

⇒
`18000`

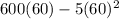
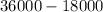
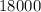
Dimensions of the rectangular area:

x = 300

y = 60