Answer:

Explanation:
The lengths of the sides of the scalene triangle are 6, 11, and 12.
We want to use the law of cosines to find the largest angle.
Note that the largest angle is always opposite the largest side.
Therefore:
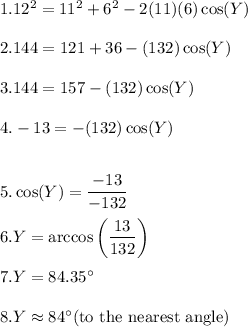
The largest angle is 84 degrees to the nearest angle.