Question

For some transformation having kinetics that obey the Avrami equation , the parameter n is known to have a value of 1.1. If, after 114 s, the reaction is 50% complete, how long (total time) will it take the transformation to go to 87% completion

y = 1 - exp(-kt^n)

Answer 1

total time = 304.21 s

Step-by-step explanation:

given data

y = 50% = 0.5

n = 1.1

t = 114 s

y = 1 - exp(-kt^n)

solution

first we get here k value by given equation

y = 1 -
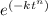`e^((-kt^n))` ...........1

put here value and we get

0.5 = 1 - e^{(-k(114)^{1.1})}

solve it we get

k = 0.003786 = 37.86 ×
`10^(4)`

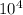
so here

y = 1 -
`e^((-kt^n))`

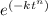
1 - y =
`e^((-kt^n))`

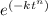
take ln both side

ln(1-y) = -k ×
`t^n`

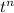
so

t =
`\sqrt[n]{-(ln(1-y))/(k)}` .............2

now we will put the value of y = 87% in equation with k and find out t

t =
`\sqrt[1.1]{-(ln(1-0.87))/(37.86*10^(-4))}`

total time = 304.21 s