Question

A thin spherical shell of radius 7.6 cm carries a uniform surface charge density of 6.7 times 10-9 C/m2. The magnitude of the electric field (in N/C) at r = 7.8 cm is approximately:___________.

Answer 1

E= 1.968 10¹¹ N/C

Step-by-step explanation:

To calculate the electric field of a sphere we can use Gaussian law

Ф = ∫ E. dA =
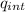`q_(int)`/ ε₀

In this case we must use a Gaussian surface of spherical shape, since the radii of the sphere and the electric field line have been parallel, consequently the scalar product is reduced to an algebraic product.

The error of a sphere is

A = 4π π r²

E (4π r³) =
`q_(int)` / εo (1)

to find the charge inside the sera we use the concept of density

ρ = quint / V

qint = rho V

the volume of a sphere is

V = 4/3 pi r³

we substitute in 1

E 4π r² = ρ 4/3 π r³

E = ρ / 3ε₀

now let's change the charge density to the charge

E = Q 3 / 4π r³ r / 3ε₀

E = (1 / 4πε₀) Q / r²

E = k Q /r²

calculate

E = ρr / 3ε₀

E = 6.7 10⁻⁹ 7.8 10⁻² / 3 8.85 10⁻¹²

E= 1.968 10¹¹ N/C