Question

A survey asks, "If the husband in a family wants children, but the wife decides that she does not want any children, is it all right for the wife to refuse to have children?" Of 705 subjects, 581 said yes. a. Find a 99% confidence interval for the population proportion who would say yes. (Use ascending order. Round to four decimal places as needed.) Can you conclude that the population proportion exceeds 75%? Why? in 2 A. No, we cannot conclude that the population proportion exceeds 75%, because 75% is below the lowest believable value of the confidence interval B. Yes, we can conclude that the population proportion exceeds 75% because 75% is above the lowest believable value of the confidence interval C. No, we cannot conclude that the population proportion exceeds 75% because 75% is above the lowest believable value of the confidence interval D. Yes, we can conclude that the population proportion exceeds 75% because 75% is below the lowest believable value of the confidence interval. b. Without doing any calculations, explain whether the interval in (a) would be wider or narrower than a 95% confidence interval for the population proportion who would say yes. The 99% confidence interval would be wider than a 95% confidence interval. The 99% confidence interval would be narrower than a 95% confidence interval.

Answer 1

a. The 99% confidence interval for the population proportion is (0.7872, 0.8610).

D. Yes, we can conclude that the population proportion exceeds 75% because 75% is below the lowest believable value of the confidence interval.

b. The 99% confidence interval would be wider than a 95% confidence interval.

As the confidence level increases, the width interval increases, as we are requiring more confidence with the same information (there is no new sample). This means that, to be more confident, the only way is to include more values in the interval.

Explanation:

We have to calculate a 99% confidence interval for the proportion.

The sample proportion is p=0.8241.

`p=X/n=581/705=0.8241`

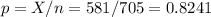
The standard error of the proportion is:

`\sigma_p=\sqrt{(p(1-p))/(n)}=\sqrt{(0.8241*0.1759)/(705)}\\\\\\ \sigma_p=√(0.000206)=0.0143`

The critical z-value for a 99% confidence interval is z=2.5758.

The margin of error (MOE) can be calculated as:

`MOE=z\cdot \sigma_p=2.5758 \cdot 0.0143=0.0369`

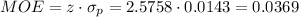
Then, the lower and upper bounds of the confidence interval are:

`LL=p-z \cdot \sigma_p = 0.8241-0.0369=0.7872\\\\UL=p+z \cdot \sigma_p = 0.8241+0.0369=0.8610`

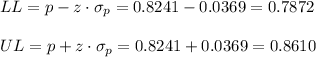
The 99% confidence interval for the population proportion is (0.7872, 0.8610).

We can conclude that there is, at least, 99% chances that the true proportion is higher than 0.7872. So there is at least 99% chances that the population proportion is higher than 0.75.