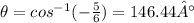Question

Find the angle between the vectors. (First find an exact expression and then approximate to the nearest degree.)

a = (1, - 4, 1)
b = (0, 2,-2)

Answer 1

`a.b = (1*0) + (-4*2) +(1*-2)= -10`

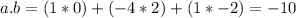
And replacing we got:

`cos \theta = (-10)/(√(18) √(8))= -(10)/(√(144))= -(10)/(12)= -(5)/(6)`

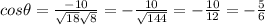
And we can find the angle with the inverse cosine function and we got:

`\theta =cos^(-1) (-(5)/(6))= 146.44°`

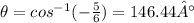
Explanation:

for this case we can use the following identity:

`cos \theta = (a.b)/(|a| |b|)`

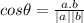
We can begin finding the norm for each vector and we got:

`|a| =√((1)^2 +(-4)^2 +(1)^2)= √(18)`

`|b| =√((0)^2 +(2)^2 +(-2)^2)= √(8)`

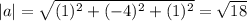
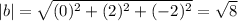
Now we can find the dot product and we got:

`a.b = (1*0) + (-4*2) +(1*-2)= -10`

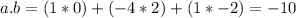
And replacing we got:

`cos \theta = (-10)/(√(18) √(8))= -(10)/(√(144))= -(10)/(12)= -(5)/(6)`

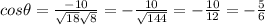
And we can find the angle with the inverse cosine function and we got:

`\theta =cos^(-1) (-(5)/(6))= 146.44°`