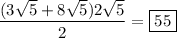Question

Hi :) how to do 10(iii) ?:)

Answer 1

(i) AB and DC are parallel, so the lines containing these sides have the same slope.

The line containing AB has slope (2 - (-1))/(10 - 4) = 3/6 = 1/2.

Use the point-slope formula to find the equation of the line containing CD:

`y-8=\frac12(x-12)\implies y=\frac x2+2\implies\boxed{2y=x+4}`

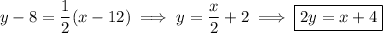
AP is perpendicular to both AB and CD, and perpendicular lines have slopes that are negative reciprocals of one another. This means the line containing AP has slope -1/(1/2) = -2. Using the point-slope formula again, the equation of the line containing AP is

`y-(-1) = -2(x-4)\implies \boxed{y=-2x+7}`

(ii) D lies on the x axis, so its y-coordinate is 0. Find the x-coordinate by plugging y = 0 into the equation for the line containing CD:

`2\cdot0=x+4\implies x=-4`

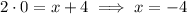
So D is the point (-4, 0).

P is the intersection of the lines containing CD and AP, so set them equal and solve for x and y :

`y=\frac x2+2\text{ and }y=-2x+7`

`\implies\frac x2+2=-2x+7\implies 5x=10\implies x=2`

`\implies y=-2\cdot2+7\implies y=3`

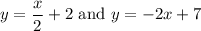
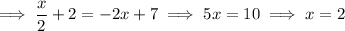
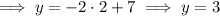
So P is the point (2, 3).

(iii) For ASBC to be a parallelogram, we need to find the coordinates of S such that the line containing AS is parallel to the line containing BC, and the line containing SC is parallel to the line containing AB.

BC has slope (8 - 2)/(12 - 10) = 6/2 = 3. Then the line containing AS has equation

`y-(-1)=3(x-4)\implies y=3x-13`

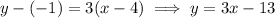
We already know AB has slope 1/2. Then the line containing SC has equation

`y-8=\frac12(x-12)\implies y=\frac x2+2`

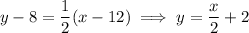
S is the intersection of these two lines:

`3x-13=\frac x2+2\implies\frac{5x}2=15\implies5x=30\implies x=6`

`\implies y=3\cdot6-13\implies y=5`

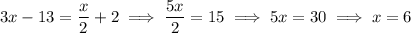
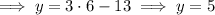
So S is the point (6, 5), and *not* (2, -7) as the answer key suggests. In fact, (2, -7) is located lower than the point A and slightly to the left; if you draw that point and connect it to the other three, there's no way to get a parallelogram.

(iv) Find the lengths of AB, CD, and AP. Then the area is (AB + CD)*AP/2.

`AB=√((4-10)^2+(-1-2)^2)=3\sqrt5`

`CD=√((12-(-4))^2+(8-0)^2)=8\sqrt5`

`AP=√((4-2)^2+(-1-3)^2)=2\sqrt5`

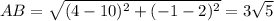
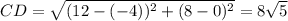
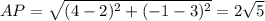
so the area is

`\frac{(3\sqrt5+8\sqrt5)2\sqrt5}2=\boxed{55}`