Question

By law, an industrial plant can discharge not more than 500 gallons of waste water per hour, on the average, into a neighboring lake. Based on other infractions they have noticed, an environmental action group believes this limit is being exceeded. Monitoring the plant is expensive, and only a small sample is possible. Four one-hour periods are selected randomly over a period of one week. The following are observed:

1384, 683, 1534, 405

Do you reject the null hypothesis that the limit is not being exceeded?

Answer 1

We conclude that not more than 500 gallons of wastewater per hour, on average, is discharged into a neighboring lake.

Explanation:

We are given that an industrial plant can discharge not more than 500 gallons of wastewater per hour, on average, into a neighboring lake.

Four one-hour periods are selected randomly over a period of one week. The following are observed:

1384, 683, 1534, 405

Let
`\mu` = population average gallons of wastewater discharged per hour

So, Null Hypothesis,
`H_0` :
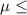`\mu \leq` 500 gallons {means that not more than 500 gallons of wastewater per hour, on the average, is discharged into a neighboring lake}

Alternate Hypothesis,
`H_A` :
`\mu` > 500 gallons {means that more than 500 gallons of wastewater per hour, on the average, is discharged into a neighboring lake}

The test statistics that will be used here is One-sample t-test statistics because we don't know about population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean =
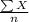`(\sum X)/(n)` = 1001.5 gallons

s = sample standard deviation =
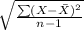`\sqrt{(\sum (X - \bar X)^(2) )/(n-1) }` = 543.79

n = sample of periods = 4

So, the test statistics =
`(1001.5-500)/((543.79)/(√(4) ) )` ~
`t_3`

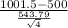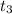
= 1.844

The value of t-test statistics is 1.844.

Since in the question we are not given with the level of significance so we assume it to be 5%. Now, at 0.05 level of significance, the t table gives a critical value of 2.353 at 3 degrees of freedom for the right-tailed test.

Since the value of our test statistics is less than the critical value of z as 1.844 < 2.353, so we have insufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that not more than 500 gallons of wastewater per hour, on average, is discharged into a neighboring lake.