Question

Esrudiantes ganaron un concurso ,lo cual el premio fue visita a fabrica de reciclaje , A mitad de la charla se retiraron 10 mujeres y se observo que el numero de varones era el doble que el de mujeres ,casi al final de la charla se retiraron 45 varones y takbiek se obeservo que el numero de mujeres era el doble que los varones ¿que cantidad de mujeres y varones estuvieron en la charla?¿cual fue el total de asistentes?

Answer 1

The total number of students who attended the talk is 100.

Explanation:

We are given that halfway through the talk, 10 women withdrew and it was observed that the number of men was twice that of women.

Then, almost at the end of the talk, 45 men withdrew and it was observed that the number of women was twice that of men.

Let the number of women who attended the talk be 'w' and the number of men who attended the talk be 'm'.

Now, according to the question;

• The first condition states that the 10 women withdrew and it was observed that the number of men was twice that of women, i.e;

`m = 2 * (w-10)`

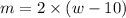
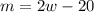`m = 2w-20` ----------------- [Equation 1]

• The second condition states that at the end of the talk, 45 men withdrew and it was observed that the number of women was twice that of men, i.e;

`(w-10) = 2(m-45)`

`w-10= 2m-90`

`w= 2m-80`

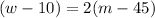
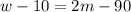
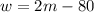
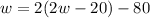`w= 2(2w-20)-80` {using equation 1}

`w= 4w-40-80`

`4w-w= 120`

`3w= 120`

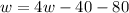
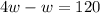
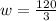`w=(120)/(3)` = 40

Now, putting the value of w in equation 1 we get;

`m = 2w-20`

`m = 2(40) -20`

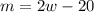
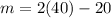
= 80 - 20 = 60

So, the number of men who attended the talk is 60 and the number of women is 40.

Hence, the total number of students who attended the talk is (60 + 40) = 100.