Question

Derive the following equations of motion

a) v=u + at
b)

`s = ut + (1)/(2) {}at^(2)`
c)

`v {}^(2) = {u}^(2) + 2as`
plz help me
​

Answer 1

___________________________________

a. Let us assume a body has initial velocity 'u' and it is subjected to a uniform acceleration 'a' so that the final velocity 'v' after a time interval 't'. Now, By the definition of acceleration, we have:

`a = (v - u)/(t) \\ or \: at = v - u \\ v = u + at \:`

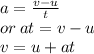
It is first equation of motion.

___________________________________

b. Let us assume a body moving with an initial velocity 'u'. Let it's final body 'v' after a time interval 't' and the distance travelled by the body becomes 's' then we already have,

`v = u + at...........(i) \\ s = (u + v)/(2) * t.........(ii)`

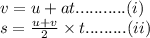
Putting the value of v from the equation (i) in equation (ii), we have,

`s= (u + (u + at))/(2) * t \: \: \\ or \: s = ((2u + at)t)/(2) \\ or \: s = \frac{2ut + a {t}^(2) }{2} \\ s = ut + (1)/(2) a {t}^(2)`

It is third equation of motion.

________________________________

c. Let us assume a body moving with an initial velocity 'u'. Let it's final velocity be 'v' after a time and the distance travelled by the body be 's'. We already have,

`v = u + at.....(i) \\ s = (u + v)/(2) * t......(ii) \\`

`v = u + at \\ or \: at = v - u \\ t = (v - u)/(a)`

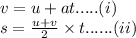
Putting the value of t from (i) in the equation (ii)

`s = (u + v)/(2) * (v - u)/(a) \\ or \: s = \frac{ {v}^(2) - {u}^(2) }{2a} \\ or \: 2as = {v}^(2) - {u}^(2) \\ {v}^(2) = {u}^(2) + 2as`

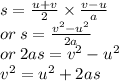
It is forth equation of motion.

________________________________

Hope this helps...

Good luck on your assignment..