Question

-4x^2+10x-8 how many distinct real number zeros does it have

Answer 1

The equation
`-4x^2+10x-8` does not have any real zeroes.

Explanation:

The given equation is
`-4x^2+10x-8`.

Let us compare it with standard quadratic equation
`ax^2+bx+c`

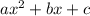
a = -4

b = 10

c = -8

The nature of zeroes is determined by Discriminant 'D'.

1. If D = 0, the quadratic equation has two equal real zeroes.

2. If D > 0, the quadratic equation has two unequal real zeroes.

3. If D < 0, the quadratic equation has two non-real or imaginary zeroes.

Formula for D is:

`D=b^(2) -4ac`

Putting the values of a, b and c to find D:

`\Rightarrow 10^2 - 4(-4)(-8)\\\Rightarrow 10^2 - 4(4)(8)\\\Rightarrow 100 - 4(32)\\\Rightarrow 100 - 128\\\Rightarrow D = -28`

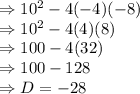
Here, D is negative so the zeroes of this quadratic equation are imaginary.

Hence, no real zeroes for the given equation
`-4x^2+10x-8`.