Question

Sketch the graph for the following quadratic function.


`- x ^(2) + 4x + 12`​
it's ok if it's wrong.i just wanna see how the work done to do this

Answer 1

Please refer to the attached image for the graph of given function.

Explanation:

Given the equation:

`-x^(2) +4x+12`

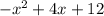
Let us rewrite by letting it equal to
`y`.

`y=-x^(2) +4x+12`

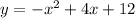
Now, we can see that it is a quadratic equation and it is known that a quadratic equation has a graph of parabola.

Let us compare the given equation with standard quadratic equation:

`y=ax^(2) +bx+c`

we get:

`a = -1\\b = 4\\c = 12`

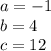
Coefficient of
`x^(2)` is negative 1, so the parabola will open downwards.

Axis of symmetry: It is the line which will divide the parabola in two equal congruent halves.

Formula for axis of symmetry is:

`x = -(b)/(2a)`

`x = -(4)/(2(-1))\\\Rightarrow x=2`

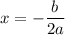
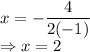
It is shown as dotted line in the image attached in the answer area.

Axis of symmetry will also contain the vertex of the parabola.

It is a downward parabola so vertex will be the highest point on this parabola.

Putting x = 2 in the equation of parabola:

`y=-2^(2) +4* 2+12\\\Rightarrow y =16`

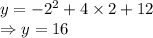
So, vertex will be at P(2, 16).

Now, let us find points of parabola to sketch graph:

put x = 0,
`y=-0^(2) +4* 0+12=12`

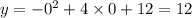
Another point is Y(0,12)

Now, let us put y = 0, it will give us two points because the equation is quadratic in x.

`0=-x^(2) +4x+12\\\Rightarrow -x^(2) +6x-2x+12=0\\\Rightarrow -x(x -6)-2(x-6)=0\\\Rightarrow (-x-2)(x-6)=0\\\Rightarrow x = -2, 6`

So, other two points are X1(-2, 0) and X2(6,0).

If we plot the points P, Y, X1 and X2 we get a graph as attached in the image in answer area.