Question

The weights of a certain brand of candies are normally distributed with a mean weight of 0.8552 g and a standard deviation of 0.0519 g. A sample of these candies came from a package containing 442 ​candies, and the package label stated that the net weight is 377.3 g.​ (If every package has 442 ​candies, the mean weight of the candies must exceed StartFraction 377.3 Over 442 EndFraction equals0.8537 g for the net contents to weigh at least 377.3 ​g.) a. If 1 candy is randomly​ selected, find the probability that it weighs more than 0.8537 g. The probability is nothing. ​(Round to four decimal places as​ needed.)

Answer 1

The probability that the weight of a candy randomly selected is more than 0.8537 is 0.7486

Explanation:

The given parameters are;

The mean candle weight = 0.8552 g

The standard deviation = 0.0519 g

The number in the sample, n = 442 candles

By central limit theorem, the sample standard deviation,
`\sigma _(\bar x)` is given by the relationship;

`\sigma _(\bar x) = (\sigma)/(√(n) ) = (0.0519)/(√(442) ) = 0.002469`

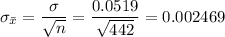
The probability is given by the relation;

`P\left (\bar{X}>0.8537 \right )= P\left (\frac{\bar{X}-\mu }{(\sigma )/(√(n))} >(0.8537-\mu )/((\sigma )/(√(n))) \right )`

`P\left (\bar{X}>0.8537 \right )= P\left (\frac{\bar{X}-0.8552 }{(\sigma )/(√(n))} >(0.8537-0.8552 )/((0.0519 )/(√(442))) \right )`

`P\left (\bar{X}>0.8537 \right )= P\left (z>-0.6076\right )`

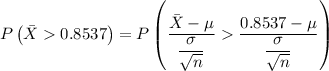
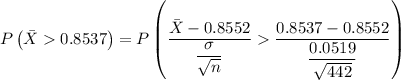
The from the z-score table we have = 0.2514

The probability of P (z > -6076) = 1 - 0.2514 = 0.7486

The probability that the weight of a candy randomly selected is more than 0.8537 = 0.7486.