Question

Jeanine Baker makes floral arrangements. She has 18 different cut flowers and plans to use 7 of them. How many different selections of the 7 flowers are​ possible?

Answer 1

31,824 different selections

Step-by-step explanation:

Since we are making selection, we will use the combination formula to find the number of selections possible.

For example, If r objects are selected from a pool of n objects, this can be done in nCr different ways.

`nCr = (n!)/((n-r)!)r! \\`

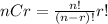
if Jeanine Baker makes floral arrangements with 18 different cut flowers and plans to use 7 of them, her selection can be made in 18C7 different ways.

`18C7 = (18!)/((18-7)!7!)\\18C7 = (18!)/(11!7!)\\ 18C7 = (18*17*16*15*14*13*12*11!!)/(11!*7*6*5*4*3*2!)\\\\18C7 = (18*17*16*15*14*13*12)/(7*6*5*4*3*2!)\\18C 7 = (3*17*16* 3*2*13)/(2) \\18C7 = 31,824\ different\ selections`