Answer:
95% confidence interval for a Population proportion
0.6937 ≤ P ≤ 0.7515
Explanation:
Explanation:-
Given sample size 'n' = 238
probability of successes or sample proportion
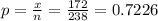
95% confidence interval for a Population proportion is determined by

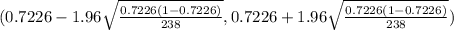
(0.7226 - 0.0289 , 0.7226 + 0.0289)
(0.6937 , 0.7515)
Conclusion:-
95% confidence interval for a Population proportion
0.6937 ≤ P ≤ 0.7515