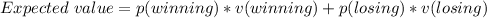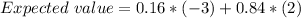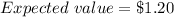Question

Taranique loves to play the floating duck game at the carnival. For $2.00 per try, she gets to choose one duck out of 50 swimming in the water. If taranique is lucky, she will pick one of the 8 winning ducks and go home with a pink teddy bear. What is the expected value of the game for Taranique if the value of the prize is $5.00?

Answer 1

$1.20

Explanation:

First we need to find the probability of winning the game.

If there are 8 winning ducks among 50 ducks, and we can pick only one, the probability of winning is 8/50 = 0.16, therefore the probability of losing the game is 1 - 0.16 = 0.84.

The player pays $2 to play, so if the player loses, the owner of the game wins $2, and if the player wins, the owner loses $3 (he receives $2 but pays the prize of $5).

Now, to find the expected value of the game, we just need to multiply the price of winning by the corresponding probability and summing with the same product but related to losing the game:

`Expected\ value = p(winning)*v(winning) + p(losing)*v(losing)`

`Expected\ value = 0.16 * (-3) + 0.84 * (2)`

`Expected\ value = \$1.20`