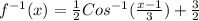Question

Determine the inverse of this function.

f(x) = 3 cos(2x – 3) + 1

Answer 1

a)
`f^(-1) (x) = (1)/(2) Cos^(-1) ((x-1)/(3) ) +(3)/(2)`

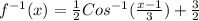
The inverse of given function

`f^(-1) (x) = (1)/(2) Cos^(-1) ((x-1)/(3) ) +(3)/(2)`

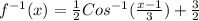
Explanation:

Step(i):-

Given function f(x) = 3 cos (2 x -3) + 1

Let y = f(x) = 3 cos (2 x -3) + 1

y = 3 cos (2 x -3) + 1

⇒ y - 1 = 3 cos (2 x -3)

⇒
`cos ( 2 x - 3 ) =(y -1)/(3)`

⇒
`cos ^(-1) ( cos (2 x - 3)) = Cos^(-1) ((y-1)/(3) )`

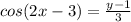
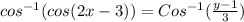
We know that inverse trigonometric equations

cos⁻¹(cosθ) = θ

`2 x - 3 = Cos^(-1) ((y-1)/(3) )`

`2 x = Cos^(-1) ((y-1)/(3) ) +3`

`x = (1)/(2) Cos^(-1) ((y-1)/(3) ) +(3)/(2)`

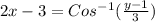
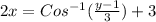
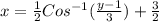
Step(ii):-

we know that y= f(x)

The inverse of the given function

`x = f^(-1) (y)`

`f^(-1) (y) = (1)/(2) Cos^(-1) ((y-1)/(3) ) +(3)/(2)`

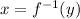
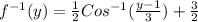
The inverse of given function in terms of 'x'

`f^(-1) (x) = (1)/(2) Cos^(-1) ((x-1)/(3) ) +(3)/(2)`

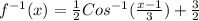
conclusion:-

The inverse of given function

`f^(-1) (x) = (1)/(2) Cos^(-1) ((x-1)/(3) ) +(3)/(2)`