Question

Which statements about the hyperbola are true? Check all that apply. A. There is a focus at (0,−10). B. There is a focus at (0, 12). C. y = x is an asymptote. D. y = x is an asymptote. E. x = is a directrix. F. y = is a directrix.

Answer 1

A. There is a focus at (0,−10).

Explanation:

Assume the hyperbola is like the one below.

The hyperbola is vertical and centred on the y-axis, so its general equation is

`(y^(2))/(a^(2)) - (x^(2))/(b^(2)) = 1`

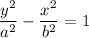
The vertices of your parabola are (0,±8) so a = 8.

The covertices are (±6,0), so b = 6.

Calculate c

`\begin{array}{rcl}a^(2) + b^(2) & = & c^(2)\\8^(2) + 6^(2) & = & c^(2)\\64 + 36 & = & c^(2)\\100 & = & c^(2)\\c & = & \mathbf{10}\\\end{array}`

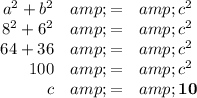
A. Foci

The foci are at (0, ±c) = (0, ±10)

TRUE. There is a focus at (0,-10).

B. Foci

The foci are at (0,±10).

False. There is no focus at (0,12)

C. and D. Asymptotes

The equations for the asymptotes are

`y = \pm(a)/(b)x = \pm(8)/(6)x = \pm(4)/(3)x`

So, y = ±x are not asymptotes.

False.

E. and F. Directrices

The equations of the directrices are

y = ±a²/c = ±64/10 = ±6.4

y = 6.4 is a directrix.

E is false. x = cannot be a directrix

F is uncertain. Your equation for the directrix is incomplete.