Answer:
The measures of the two angles are 80 and 100
Explanation:
Let
 and
and
 represent the two angles such that
represent the two angles such that
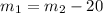
Required
Find
 and
and

The two angles of a same-side interior angle of parallel lines add up to 180;
This implies that
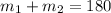
Substitute
 for
for

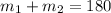 becomes
becomes
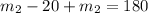
Collect like terms
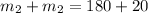
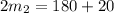
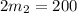
Divide both sides by 2
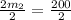
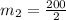
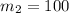
Recall that
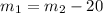
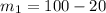
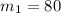
Hence, the measures of the two angles are 80 and 100