Question

HELP ASAP HELP PLEASE ASAP

Answer 1

WXYZ can not be a rectangle because consecutive sides are not perpendicular to each other.

Explanation:

The given vertices are W(-4,3), X(1,5), Y(3,1) and Z(-2,-1).

Plot these points on coordinate plane and draw the quadrilateral as shown below.

`Slope=(y_2-y_1)/(x_2-x_1)`

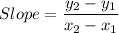
Using this formula, we get

`m_(WX)=(5-3)/(1-(-4))=(2)/(5)`

`m_(XY)=(1-5)/(3-1)=(-4)/(2)=-2`

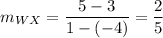
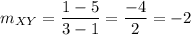
Now,

`m_(WX)* =(2)/(5)* (-2)=-(4)/(5)\\eq -1`

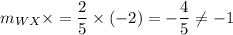
Here, WX and XY are two consecutive sides of quadrilateral but the product of their slopes is not equal to -1. It means they are not perpendicular to each other.

Since, all interior angles of a rectangle are right angles, therefore, WXYZ can not be a rectangle.