Question

Circle X with a radius of 6 units and circle Y with a radius

of 2 units are shown.
Which steps would prove the circles similar?
6
0 Translate the circles so they share a common center
point, and dilate circle Y by a scale factor of 4.
0 Translate the circles so the center of one circle rests
on the edge of the other circle, and dilate circle Y by a
scale factor of 4.
Y
0 Translate the circles so they share a common center
point, and dilate circle Y by a scale factor of 3.
Os Translate the circles so the center of one circle rests
on the edge of the other circle, and dilate circle Y by a
scale factor of 3.​

Answer 1

the answer is c

Explanation:

Translate the circles so they share a common center point, and dilate circle Y by a scale factor of 3.

edge 2020-2021

Answer 2

Option C.

Explanation:

It is given that radius of circle X is 6 units and radius of circle Y is 2 units.

Here, circle Y is smaller and circle X is larger.

`\text{Scale factor}=\frac{\text{Radius of circle X}}{\text{Radius of circle Y}}`

`\text{Scale factor}=(6)/(2)`

`\text{Scale factor}=3`

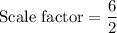
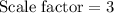
If we translate the circles so they share a common center point, and after that we dilate circle Y by a scale factor of 3, then we get circle which is equal to circle X.

We know that, after dilation the figure and its image are similar.

Hence, we can say that both circles are similar.

Therefore, the correct option is C.