Answer:
The interval is constructed at 93% confidence.
Explanation:
Confidence interval concepts:
A confidence interval has two bounds, a lower bound and an upper bound.
A confidence interval is symmetric, which means that the point estimate used is the mid point between these two bounds, that is, the mean of the two bounds.
The margin of error is the difference between these two bounds, divided by 2.
Confidence interval of proportions concepts:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
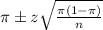
In which
z is the zscore that has a pvalue of
 .
.
The margin of error is:
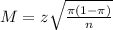
In this problem, we have that:
2050 people, so n = 2050.
Lower bound: 0.878
Upper bound: 0.903
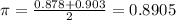
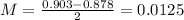
Confidence level:
We have to find z.
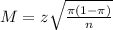
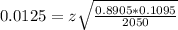
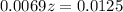
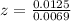
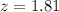
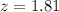 has a pvalue of 0.965.
has a pvalue of 0.965.
That is:
![]1 - (\alpha)/(2) = 0.965](https://img.qammunity.org/2021/formulas/mathematics/college/cgv19pz9goifc0hogc5lcvztxm8bgctm89.png)
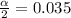

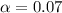
Finally
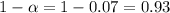
The interval is constructed at 93% confidence.