Answer:
Therefore, domain of y =
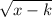 ; Domain = [k, ∞)
; Domain = [k, ∞)
Domain of y =
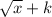 ; Domain = [0, ∞)
; Domain = [0, ∞)
Explanation:
Two functions are,
y =
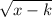
and y =

Let the value of k = 1
Then we find the graph of the functions attached.
By analyzing these graphs,
y =
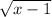 when shifted 1 unit right and 1 unit down we get a new function,
when shifted 1 unit right and 1 unit down we get a new function,
y =
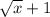
Therefore, domain of y =
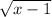 ; Domain = [1, ∞)
; Domain = [1, ∞)
Domain of y =
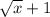 ; Domain = [0, ∞)
; Domain = [0, ∞)
Similarly, domain of y =
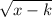 ; Domain = [k, ∞)
; Domain = [k, ∞)
And domain of y = √x + k ; Domain = [0, ∞)