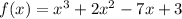Answer:
(a)Degree 3
(b)
Step-by-step explanation:
(a)Given the function represented by the set of points: {(-3,15)(-2,17), (-1,11), (0,3),(1,-1), (2,5),(3,27)}.
To determine the degree of the polynomial of the function, we plot the function on a graph.
From the graph, the function has 2 turning points.
The maximum number of turning points of a polynomial function is always one less than the degree of the function.
Therefore, the polynomial has a degree of 3 .
(b)A cubic function is one in the form where d is the y-intercept.
A cubic function is one in the form
 where d is the y-intercept.
where d is the y-intercept.
- From the point (0,3) the y-intercept, d=3
Therefore, our polynomial is of the form:
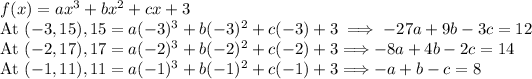
Solving the three resulting equations simultaneously (using a calculator), we obtain:
a=1, b=2, c=-7
Therefore, the equation for this function is: