Question

Solve cosθ-cos2θ+cos3θ-cos4θ=0

Answer 1

• θ = (2/5)πk or π(k +1/2) . . . . . for any integer k

Explanation:

We can make use of the identities ...

`cos(\alpha)-cos(\beta)=-2\sin{(\alpha+\beta)/(2)}\sin{(\alpha-\beta)/(2)}\\\\sin(\alpha)+sin(\beta)=2\sin{(\alpha+\beta)/(2)}\cos{(\alpha-\beta)/(2)}`

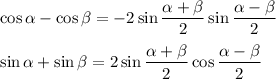
These let us rewrite the equation as ...

`0=cos(\theta)-cos(2\theta)+cos(3\theta)-cos(4\theta)\\\\0=-2\sin{(\theta+2\theta)/(2)}\sin{(\theta-2\theta)/(2)}-2\sin{(3\theta+4\theta)/(2)}\sin{(3\theta-4\theta)/(2)}\\\\0=2\sin{(\theta)/(2)}\left(\sin{(3\theta)/(2)}+\sin{(7\theta)/(2)}\right)\\\\0=4\sin{(\theta)/(2)}\sin{(3\theta+7\theta)/(4)}\cos{(3\theta-7\theta)/(4)}\\\\0=4\sin{(\theta)/(2)}\sin{(5\theta)/(2)}cos(\theta)`

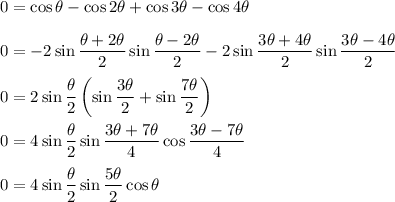
The solutions are the values of θ that make the factors zero. That is, ...

θ = 2πk . . . . for any integer k

θ = (2/5)πk . . . . for any integer k (includes the above cases)

θ = π(k +1/2) . . . . for any integer k