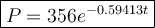Answer:
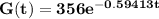
Explanation:
Use the decay formula:
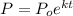 where
where
- P is the remaining amount of the sample
- P₀ is the original amount of the sample
- k is the decay rate
- t is the time (in hours)
Given: P = 44.5, P₀ = 356, k = unknown, t = 210 minutes (3.5 hours)
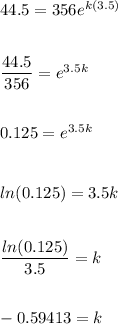
Input P₀ = 356 and k = -0.59413 into the decay formula