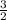Answer:
h = -
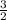
Explanation:
The equation of a parabola in vertex form is
y = a(x - h)² + k
where (h, k) are the coordinates of the vertex and a is a multiplier
Given
y = 2x² + 6x + 11 ( factor out 2 from the first 2 terms )
= 2(x² + 3x) + 11
Using the method of completing the square
add/subtract ( half the coefficient of the x- term )² to x² + 3x
y = 2(x² + 2(
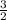 )x +
)x +
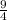 -
-
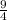 ) + 11
) + 11
= 2(x +
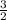 )² -
)² -
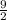 + 11
+ 11
= 2(x +
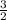 )² +
)² +
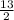 ← in vertex form
← in vertex form
with h = -