Question

A geometric series has the third term 36 , and sixth term 972 . Find the first term of the series

Answer 1

a₁ = 4

Explanation:

The n th term of a geometric series is

`a_(n)` = a₁
`r^(n-1)`

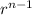
where a₁ is the first term and r the common ratio

Given a₃ = 36 and a₆ = 972 , then

ar² = 36 → (1)

a
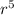`r^(5)` = 972 → (2)

Divide (2) by (1)

`(ar^(5) )/(ar^(2) )` =
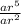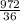`(972)/(36)` , that is

r³ = 27 ( take the cube root of both sides )

r =
`\sqrt[3]{27}` = 3

Substitute r = 3 into (1)

9a = 36 ( divide both sides by 9 )

a = 4

The first term is 4

Answer 2

the first term is 4

Explanation:

Given

G(3) = 36

G(6) = 972

Solution:

General formula for geometric series

G(x) = AB^x

From given data: G(6)/G(3) = 972/36 = 27

From formula: G(6)/G(3) = AB^6/(AB^3) = B^3

Therefore

B^3 = 27

B=3

Hence

G(1) = AB^1 = AB^3/B^2=36/3^2=36/9=4

Ans: the first term is 4