Answer:
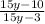
Explanation:
First at all, we need to use
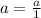to convert this expression into a fraction, like:
to convert into
.
Expand the fraction to get the least common denominator, like
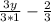
Write all numerators above the common denominator, like this:
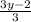
The bottom one used the same way to became simplest form, like this:
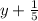
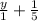
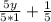
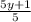
And it became like this:
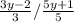
Now, we are going to simplify this complex fraction. We can use cross- multiply method to simplify this fraction.
3y-2(5) and 5y-1(3)
and it will becomes like this in function form:
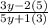
Then, we should distribute 5 through the parenthesis
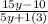
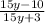
And.... Here we go. That is the answer.