Answer:
1
Explanation:
First, convert all the secants and cosecants to cosine and sine, respectively. Recall that
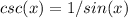 and
and
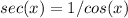 .
.
Thus:
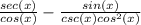
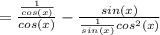
Let's do the first part first: (Recall how to divide fractions)
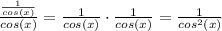
For the second term:
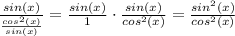
So, all together: (same denominator; combine terms)
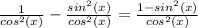
Note the numerator; it can be derived from the Pythagorean Identity:
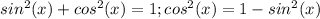
Thus, we can substitute the numerator:
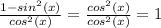
Everything simplifies to 1.