Question

2 Points

Find the solution(s) to the system of equations. Select all that apply.
y = x2 - 2x-3
y = 2x - 3
O A. (0,-3)
B. (-1,0)
C. (3,0)
D. (4,5)

Answer 1

A (0,-3) and D(4,5)

Explanation:

Given system of equations

y = x2 - 2x-3

y = 2x - 3

Solution to these will be value of x for which value of y in both equation will same.

In graph, solution will point at which curve of both equation intersect each other

To solve this we will equate the two equations

`x^2 - 2x-3 = 2x-3\\ =>x^2 - 2x-3 -2x + 3 = 0\\=> x^2 - 2x - 2x -3 + 3 = 0\\\=> x^2 - 4x = 0\\=>x(x-4) = 0\\Thus\\x = 0 \ or \ x-4 = 0\\x = 0 \ or \ x = 4`

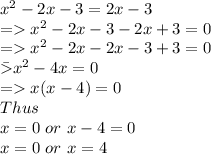
Thus, value of x is 0 and 4

we will put this value in given set of equation.

y = 2x- 3

taking x = 0

y = 2*0 -3 = 0-3 = -3

one solution is (0,-3)

taking x = 4

y = 2*4 - 3 = 8-3 = 5

Another solution is (4,5).

Though , the problem is solved we will see it this value satisfies other equation or not better understanding

y = x^2 - 2x-3

taking x = 0

y = 0^2 - 2*0-3 = -3

one solution (0,-3)

taking x = 4

y = 4^2 - 2*4-3 = 16-8 -3 = 8-3 = 5

other solution (4,5)

thus, we see both equation gives same set of solution.