Answer:
Explanation:
Hello,
there is not always an intersection point
let's take the example of on the appropriate domain
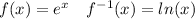
there is no intersection point
if there is one it means that the point (x,f(x)) and the point (x,
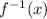 ) is the same so that have to solve
) is the same so that have to solve
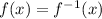
for instance if we take

intersection point are for x >= 0
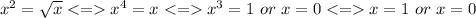
hope this helps