Question

Can anyone explain how you got the answer please.

Answer 1

Option A

Explanation:

The first thing we want to do here is identify whether or not the diagonals are perpendicular, which helps much to know to prove what angle AOB.

_____

Let us say that this is a rhombus. That would make the diagonals perpendicular, and hence ∠AOB should be 90 degrees, but let's not jump to conclusions. We need to calculate the length of BO. By Pythagorean Theorem it should be the following length -

`( BC )^2 = ( BO )^2 + ( OC )^2,\\( 10 )^2 = ( BO )^2 + ( 7.8 )^2,\\100 = BO^2 + 60.84,\\BO^2 = 39.16,\\\\BO = ( About ) 6.26\\`

_____

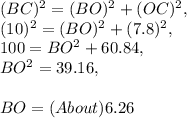
Knowing BO, to prove that this is a rhombus we can find the length of BO another way, and match it to the length 6.26 -

Δ ABD = Equilateral,

BD = 10 cm,

" Coincidence Theorem " - BO = 5 = OD.

Here BO = 5. 5 is close to 6.26 but not exactly, so the measure of angle AOB is not 90, but better yet 80.