Question

Using the geometric mean and Pythagorean theorem, calculate the values of the missing sides. Round your answers to the thousandths place (3 decimal places).

Answer 1

a = 9.849

b = 20.25

c = 491.03

Explanation:

By using Pythagoras theorem in the right triangle BDC,

(Hypotenuse)² = (Leg 1)² + (Leg 2)²

BC² = BD² + DC²

a² = 9² + 4²

a =
`√((81+16))`

a =
`√(97)`

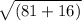
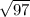
a = 9.8489

a ≈ 9.849 units

By mean proportional theorem,

`\frac{\text{DC}}{\text{BD}}=\frac{\text{BD}}{\text{AD}}`

AD × DC = BD²

b × 4 = 9²

b =
`(81)/(4)`

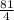
b = 20.25 units

BY Pythagoras theorem in ΔADB,

AB² = AD² + BD²

c² = b² + 9²

c² = (20.25)² + 9²

c² = 410.0625 + 81

c = 491.0625

c = 491. 063 units