Answer:
The arc length is 185.39 meters.
Explanation:
The arc length is calculated by the following expression:

Where:
 - Radius, measured in meters.
- Radius, measured in meters.
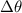 - Central angle, measured in radians.
- Central angle, measured in radians.
If
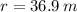 and
and
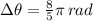 , the arc length, measured in meters, is:
, the arc length, measured in meters, is:
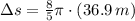
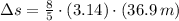
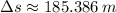
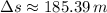
The arc length is 185.39 meters.