Hey there! :)
Answer:

Explanation:
We are given the equation:
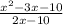
Factor the numerator and denominator:
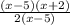
'x - 5' is on both the numerator and denominator, so it gets cancelled out and becomes a "hole".
This means that at x = 5, there is a hole. There is a limit at x ⇒ 5. Find the hole by plugging 5 into the simplified equation:
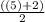 = 7/2
= 7/2
Therefore:
