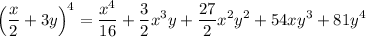Question

Use the bionomial theorem to write the binomial expansion


`( (1)/(2)x + 3y) ^(4)`
​

Answer 1

Answer:
`\bold{(1)/(16)x^4 + (3)/(2)x^3y + (27)/(2)x^2y^2 +54xy^3+81y^4}`

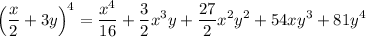
Explanation:

Binomial Tree

n=0 1

n=1 1 1

n=2 1 2 1

n=3 1 3 3 1

n=4 1 4 6 4 1

Using the Binomial Theorem

`\bigg((1)/(2)x+3y\bigg)^4\\\\\\=1\bigg((1)/(2)x\bigg)^4(3y)^0\quad \rightarrow \quad (1)/(16)x^4\\\\+4\bigg((1)/(2)x\bigg)^3(3y)^1\quad \rightarrow \quad (3)/(2)x^3y\\\\+6\bigg((1)/(2)x\bigg)^2(3y)^2\quad \rightarrow \quad (27)/(2)x^2y^2\\\\+4\bigg((1)/(2)x\bigg)^1(3y)^3\quad \rightarrow \quad 54xy^3\\\\+1\bigg((1)/(2)x\bigg)^0(3y)^4\quad \rightarrow \quad 81y^4`

______________________

`= (1)/(16)x^4 + (3)/(2)x^3y + (27)/(2)x^2y^2 +54xy^3+81y^4`

Answer 2

`$\left((x)/(2) + 3 y\right)^(4)=(x^(4))/(16) + (3)/(2) x^(3) y + (27)/(2) x^(2) y^(2) + 54 x y^(3) + 81 y^(4)$`

Explanation:

`$\left((1)/(2)x+3y \right)^4=\left((x)/(2)+3y \right)^4\\$`

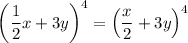
Binomial Expansion Formula:

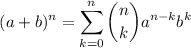`$(a+b)^n=\sum_(k=0)^n \binom{n}{k} a^(n-k) b^k$`, also
`$\binom{n}{k}=(n!)/((n-k)!k!)$`

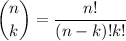
We have to solve
`$\left((x)/(2) + 3 y\right)^(4)=\sum_(k=0)^(4) \binom{4}{k} \left(3 y\right)^(4-k) \left((x)/(2)\right)^k$`

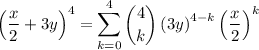
Now we should calculate for
`k=0, k=1, k=2, k=3 \text{ and } k =4;`

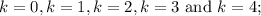
First, for
`k=0`

`$\binom{4}{0} \left(3 y\right)^(4-0) \left((x)/(2)\right)^(0)=(4!)/((4-0)! 0!)\left(3 y\right)^(4) \left((x)/(2)\right)^(0)=(4!)/(4!)(81y^4)\cdot 1 =81 y^(4)$`

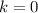
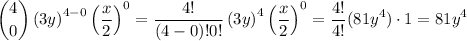
It is the same procedure for the other:

For
`k=1`

`$\binom{4}{1} \left(3 y\right)^(4-1) \left((x)/(2)\right)^(1)=54 x y^(3)$`

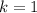
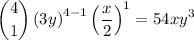
For
`k=2`

`$\binom{4}{2} \left(3 y\right)^(4-2) \left((x)/(2)\right)^(2)=(27)/(2) x^(2) y^(2)$`

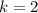
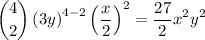
For
`k=3`

`$\binom{4}{3} \left(3 y\right)^(4-3) \left((x)/(2)\right)^(3)=(3)/(2) x^(3) y$`

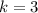
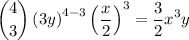
For
`k=4`

`$\binom{4}{4} \left(3 y\right)^(4-4) \left((x)/(2)\right)^(4)=(x^(4))/(16)$`

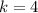
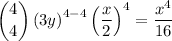
You can perform the calculations, I will not type everything.

The answer is the sum of elements calculated.

Just organizing:

`$\left((x)/(2) + 3 y\right)^(4)=(x^(4))/(16) + (3)/(2) x^(3) y + (27)/(2) x^(2) y^(2) + 54 x y^(3) + 81 y^(4)$`