Question

The lengths of the sides are in centimeters. The area of triangle A is equal to the area of triangle B.Work out the value of x, giving your answer in the form a ± √b where a and b are integers.

Answer 1

hg

Explanation:

Answer 2

The value of x, given that the area of triangle A is equal to the area of triangle B is
`1\pm (√(20))/(2)`

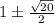
• a = 1
• b =
  `√(20)`

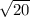
How to calculate the value of x, a and b?

First, we shall obtain the area of A and B. Details below:

For triangle A,

• Side a = x
• Side b = x
• Angle C = 30 degrees
• Area of A =?

`Area\ of\ A = (ab)/(2)SineC\\\\ = (x\ *\ x)/(2)Sine30\\\\ = (x^2)/(2)\ *\ (1)/(2) \\\\ = (x^2)/(4)`

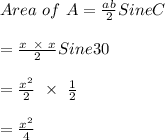
For triangle B,

• Base (b) = 1 cm
• Height (h) = x + 2
• Area of B =?

`Area\ of\ B = (1)/(2)bh\\\\ = (1)/(2)\ *\ 1\ *\ (x +2)\\\\ = (x +2)/(2)`

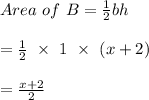
Now, we shall determine the value of x, a and b. Details below:

Area of A = Area of B

`(x^2)/(4) = (x+2)/(2)\\\\2x^2 = 4(x+2)\\\\x^2 = 2(x+2)\\\\x^2 = 2x+4\\\\x^2 - 2x - 4 = 0\\\\Solving\ with\ formula,\ we\ have:\\\\x = (-b\ \pm\ √(b^2 - 4ac))/(2a) \\\\x = (-(-2)\ \pm\ √((-2)^2\ -\ (4\ *\ 1\ *\ -4)))/(2\ *\ 1)\\\\x = (2\ \pm\ √(4\ +\ 16))/(2)\\\\x = (2\ \pm\ √(20))/(2)\\\\x = (2)/(2)\pm (√(20))/(2)\\\\x = 1\pm (√(20))/(2)\\\\Thus,\\\\a = 1\\\\b = √(20)`